Äääh, ja.
(Glaub ich)
:Lachen2:

Jo, die Richtung stimmt ... ;)

Die Abkehr vom Konkurrenz-Gedanken (Differenzen) hin zum Teamgeist (Summen) führt zu dem, was mir als schönste Lösung erscheint :

Zusammen sind Schnodo und Flow bis zum ersten Treffen die einfache Strecke einmal abgefahren, bis zum zweiten Treffen insgesamt dreimal. Da sie mit konstanter Geschwindigkeit unterwegs sind, ist auch Flow bis zum zweiten Treffen dreimal so viel gefahren wie bis zum ersten, sprich 120km (3x 40km). Gleichzeitig entspricht das der einfachen Strecke (Hinweg) plus 30km, welche damit 90km beträgt (120km - 30km).


Einfacher geht es, glaube ich, nicht ... :)

Ein bißchen einfache Streichholz-Geometrie bis wieder was besseres kommt :

Wieviele Streichhölzer braucht man mindestens, um vier gleichgroße gleichseitige Dreiecke zu bilden ?

Ich biete sechs an, und hätte noch zwo gleichseitige Dreiecke über damit, allerdings auch noch ein gleichseitiges Sechseck...:Lachen2:

Sechs ist gut. Jetzt der Längenvergleich ... :cool:

Haben sie die Seitenlänge "ein Streichholz" ?

Nein, natürlich nicht.
Es liegen zwei Dreiecke übereinander als sechszackiger Stern...;)


In deinem Sinne werf ich mal 'Neun' als Antwort in den Raum: gleichseitiges Dreieck mit Kantenlänge zwo Hölzer, darin ein weiteres aus drei Hölzern, welches das Grosse Dreieck in vier kleine unterteilt.

Was anderes hätte mich auch gewundert ... aus den Köpfen dann noch eben ein neues Schaltwerk gebaut ... :Lachen2:

Neun, wer bietet weniger ?

Das wären sogar 5 aus 9. Für 4 aus 9 kann man ja eine Vielzahl von Formen legen. 3 fürs erste und dann je 2 für jedes weitere unter Wiederverwendung je einer vorhandenen Kante.

Obacht Lösung:

6 Streichhölzer ist schon richtig!

Man lege ein Dreieck und stelle in jede Ecke ein Streichholz.

Diese treffen sich dann in einem Punkt, sieht bisschen aus wie ein Zelt/Pyramide.

Sollten 4 gleischenklige Dreiecke mit Kantenlänge "Streichholz" sein.

Gruß

Flo

Wie schön! :)

Jetzt hinterher, wenn ich das so lese, meine ich schon, da hätte man drauf kommen können. :Lachen2:

Könnte man vielleicht als threadspezifische Signatur einbauen ... :Lachen2:

Richtig.

Das nächste Mal die Lösung vielleicht irgendwie "verschleiern", dann können andere auch noch rätseln ... ;)

Geht jemand mal zu Arne und bestellt uns einen [spoiler]-Tag ?

:)

Erledigt :Huhu:

Auch das mit dem Spoiler-Tag?
F**k - ich bin einfach zu sehr in meiner 2D-, Schwarz-weiß- und Mono-Welt gefangen :(. Gute Lösung :).

Es hätte mich aufmerksam machen sollen, dass in der Aufgabe von 'bilden', nicht 'legen' die Rede war...:-((
Unterwegs aufm Rad bin ich n paar Sachen im Kopf durchgegangen und mir fiel auf, dass 9 nicht so der Bringer sind wie ich zuerst dachte.
Schlicht, weil man damit jede Menge Figuren mit 4 gleichseitigen Dreiecken LEGEN kann...

Hier mal wieder was Einfaches:

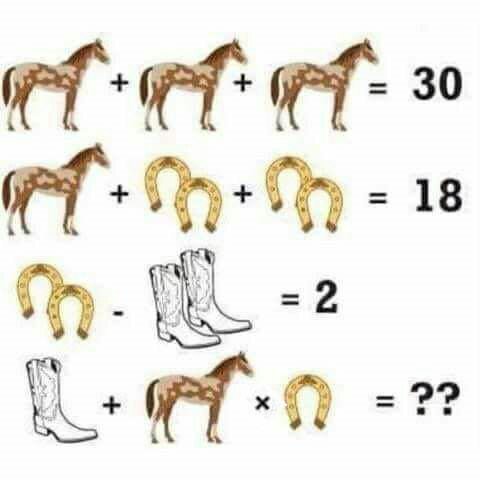so - mein Beitrag:

Drei Cowboys wurden von Indianern gefangen genommen und an drei Marterpfähle gefesselt. Die Marterpfähle stehen in einer Reihe und die Cowboys sind jeweils so angebunden, dass der am hinteren Marterpfahl angebundene Cowboy seine zwei Vordermänner von hinten sehen kann. Der am mittleren Marterpfahl angebundene Cowboy kann lediglich seinen Vordermann von hinten sehen. Der am vorderen Marterpfahl gefesselte Leidensgenosse kann keinen seiner zwei Mitgefangenen sehen. Der Häuptling zieht fünf Adlerfedern aus seiner Feldtasche, drei schwarze und zwei weiße. Er zeigt die fünf Federn den drei Cowboys. Dann steckt er jedem der drei Gefangenen eine der Federn so an den Hut, dass die Farbe der Feder von hinten zwar erkennbar ist, der Hutträger aber selbst die Feder nicht sehen kann. Die restlichen zwei Federn steckt der Häuptling wieder ein, ohne dass einer der Cowboys erkennen kann, welche Farbe diese zwei Federn haben.

Der Häuptling spricht zu den Gefangenen: "Wenn einer von euch herausfinden kann, welche Farbe die Feder auf seinem eigenen Hut hat, lasse ich euch alle frei." Dass Absprachen zwischen den drei Cowboys nicht gestattet sind, versteht sich wohl von selbst.
Sehr lange schweigen die Cowboys. Dann verkündet einer von ihnen die rettende Antwort.

Welcher der drei Cowboys kann schließlich das Rätsel lösen und welche Farbe hat die Feder an seinem Hut?

Der vorderste Cowboy hat eine schwarze Feder.

Gruß Matthias

PS: Ich sage aber jetzt nicht, wie man drauf kommt, um den Spaß nicht zu verderben.

danke :Blumen:

Ich stimme MatthiasR zu. :)


Es gibt sieben Möglichkeiten (links ist hinten):

1. Schwarz - Schwarz - Schwarz
2. Schwarz - Schwarz - Weiß
3. Schwarz - Weiß - Schwarz
4. Schwarz - Weiß - Weiß
5. Weiß - Schwarz - Schwarz
6. Weiß - Schwarz - Weiß
7. Weiß - Weiß - Schwarz

Bei 4. hätte sich sofort der Hintere gemeldet und gesagt, dass er eine schwarze Feder hat. Bei 2. und 6. hätte der Mittlere gewußt, dass er eine schwarze Feder hat, weil ansonsten der Hintere was gesagt hätte.
Es bleiben also noch die Fälle 1, 3, 5, und 7. In denen hat der Vordere immer eine schwarze Feder. Und weil er nichts von den anderen gehört hat, kennt er die Farbe. :)

Jupp, seh ich auch so.

Klassisches Rätsel:
Andi (A), Bernd (B) und Charlie (C) vereint eine alte Feindschaft. Diese wollen sie, am besten mit den Opponenten, endlich begraben. Sie treffen sich im Morgengrauen mit jeweils einer Pistole und unendlich Munition.
Andi trifft immer mit 33% Wahrscheinlichkeit, Bernd mit 66% Wahrscheinlichkeit und Charlie trifft immer.

Sie einigen sich darauf, dass sie immer abwechselnd schießen (also ABCABC...) bis nur noch einer übrig ist.

Schlechte Nachricht: Du bist Andi.
Gute Nachricht: Du darfst anfangen.

Frage: Was machst Du, um mit der größten Wahrscheinlichkeit zu gewinnen?

21

4Zeichen

Sicher bei der Lösung? Denk nochmal nach. :)

Nö, dreimal die Farbe geändert und die zwote Ziffer dabei mit weggedrückt, hüstel...
Oder die erste und hinten wieder hingeschrieben.

Was? :Gruebeln:

So schaut es aber besser aus. :)

Das kenne ich leider schon, deswegen darf ich nichts beitragen. :)

Unterwegs grad überlegt und eben noma nachgeschaut, 22 kommt tatsächlich auch dann raus, wenn man 'Punkt vor Strich' missachtet. Peinlich...:-((

Dann stelle ich mich auch mal bloß: Ich habe beim ersten Mal das x nicht erkannt und ein + angenommen. ;)

Ich sehe aber auch sehr schlecht, das will ich noch zu meiner Verteidigung sagen. Vielleicht sollte ich mal wieder zu Fielmann. :Cheese:

Versteh ich jetzt nicht. Wer schiesst auf was oder wen?
Immer zwei gleichzeitig auf den jeweils andern?
Dann würd ich als A nicht gern mit C anfangen...

Jeder schießt wohin er will, aber die Reihenfolge muss eingehalten werden. Gleichzeitig geht deshalb nicht.

Ging mir im ersten Durchgang so, ist mir aber beim Überprüfen aufgefallen mit nem Ausrufezeichen! "Punkt vor Strich!"
Deswegen isses ja so peinlich.


Bei der Schiesserei blick ich immer noch nicht, wie es gemeint ist.

A schießt auf ein beliebiges Ziel (Trefferwahrscheinlichkeit 1/3).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt - Wahrscheinlichkeit 2/3).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt - Wahrscheinlichkeit 1).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt B auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt C auf ein beliebiges Ziel (wenn er noch lebt).
Danach schießt A auf ein beliebiges Ziel (wenn er noch lebt).


Irgendwann bleibt halt nur noch einer übrig. Der hat gewonnen.

Wie muss sich A verhalten um seine Überlebenswahrscheinlichkeit zu maximieren?

Dann würde ich als A schonmal nicht auf B schiessen, denn wenn ich (zwar nur mit 1/3 Wahrscheinlichkeit) treffe, bin ich anschliessend mit 100% Wahrscheinlichkeit tot wenn C schiesst.
Denn würde B, sollte ich als A ihn nicht treffen, auf mich schiessen und treffen, würde er anschliessend ebenso von C erschossen.

Aus Sicht von Schütze B ists ähnlich: würde er auf mich (A) schiessen und treffen, würde er anschliessend sicher von C erschossen werden.

Geht man nun davon aus, dass A und B beide C nicht treffen, bleibt das Spiel offen, für wen sich C entscheiden würde.

Eventuell könnte A seine Überlebenswahrscheinlichkeit noch steigern, wenn er nicht direkt auf C zielt, sondern leicht neben ihn??

Das klingt für mich wenig sinnvoll für A.
Selbst wenn B noch lebt, stehen die Chancen bestenfalls Fifty-Fifty, dasses mir noch genauso geht, wenn C das nächste mal an der Reihe ist.

C würde natürlich auf B schießen, weil von dem die größere Gefahr ausgeht. Daraus folgt:

Wenn A in der ersten Runde auf C schießt, überlebt er mit einer Wahrscheinlichkeit von 7/9 diese Runde. Wenn er auf B schießen würde, wären es nur 2/3.

ABER: Wenn er in der ersten Runde in die Luft schießt, überlebt er diese Runde auf jeden Fall! Denn B muss ja auf C schießen und falls er nicht trifft, wird C auf B schießen.

Gruß Matthias

Das würde ich nicht als gegeben ansehen. Weder dass C auf B schiessen wird/würde, noch, dass B auf C schiessen wird.

Der einzige sinnvolle Ansatz, in die Luft zu schiessen wäre, dass A dabei mit 2/3 Wahrscheinlichkeit nicht trifft.
Sollen wir daraus folgern, dass die Wahrscheinlichkeit, stattdessen B oder gar C zu treffen mit 1/3 in die Bilanz eingeht?
:Cheese:

Das Rätsel macht nur Sinn, wenn alle überleben wollen und entsprechend rational handeln. Und da gibt es für B und C nur eine sehr klare Möglichkeit.
Nur für A ist es nicht ganz offensichtlich...